Solve the followings Questions.

1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.

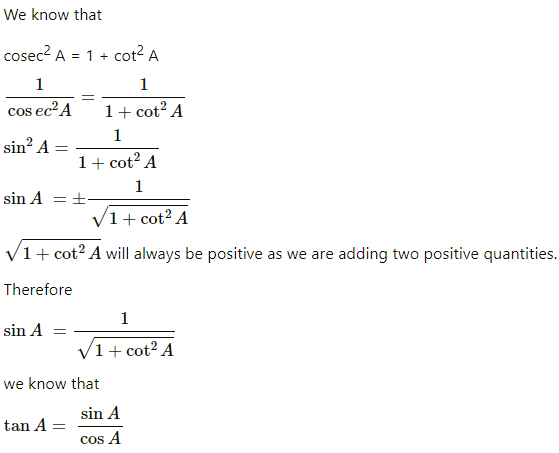
2. Write all the other trigonometric ratios of ∠A in terms of sec A.

Answer:

3. Evaluate :

(i) (sin²63° + sin²27°)/(cos²17° + cos²73°)
(ii)  sin 25° cos 65° + cos 25° sin 65°

Answer:

 (i) (sin²63° + sin²27°)/(cos²17° + cos²73°)

(ii)  sin 25° cos 65° + cos 25° sin 65°

Choose the correct option. Justify your choice.

4. (i) 9 sec²A – 9 tan²A =
(A) 1                 (B) 9        (C) 8                (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(A) 0                 (B) 1        (C) 2                (D) – 1
(iii) (secA + tanA) (1 – sinA) =
(A) secA           (B) sinA   (C) cosecA      (D) cosA
(iv) 1+tan²A/1+cot²A =
(A) sec²A          (B) -1      (C) cot²A                (D) tan²A

Answer:

(i)  (i) 9 sec²A – 9 tan²A =

(A) 1                 (B) 9        (C) 8                (D) 0 

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(A) 0                 (B) 1        (C) 2                (D) – 1

(iii) (secA + tanA) (1 – sinA) =
(A) secA           (B) sinA   (C) cosecA      (D) cosA

(iv) 1+tan²A/1+cot²A =
(A) sec²A          (B) -1      (C) cot²A                (D) tan²A

5. Prove the following identities, where the angles involved are acute angles for which the

expressions are defined.
(i) (cosec θ – cot θ)² = (1-cos θ)/(1+cos θ)
(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]
(iv) (1 + sec A)/sec A = sin²A/(1-cos A)  
[Hint : Simplify LHS and RHS separately]
(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A,using the identity cosec²A = 1+cot²A.

(vi) √1 + sin A/1 – sin A = sec A+ tan A

(vii) (sin θ – 2sin³θ)/(2cos³θ-cos θ) = tan θ

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7+tan²A+cot²A
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
 [Hint : Simplify LHS and RHS separately]
(x) (1+tan²A/1+cot²A) = (1-tan A/1-cot A)² = tan²A

Answer:

(i) (cosec θ – cot θ)² = (1-cos θ)/(1+cos θ)

(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A 

(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ

[Hint : Write the expression in terms of sin θ and cos θ]

(iv) (1 + sec A)/sec A = sin²A/(1-cos A)  

[Hint : Simplify LHS and RHS separately] 

(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A,using the identity cosec²A = 1+cot²A

(vi) √1 + sin A/1 – sin A = sec A+ tan A

LHS = 1 + sin A/(1 – sin A) …..(1)

Multiplying and dividing by (1 + sin A)

⇒ (1 + sin A)(1 + sin A/1 – sin A)(1 + sin A)

= (1 + sin A)²/(1 – sin² A) [a² – b² = (a – b)(a + b)]

= (1 + sinA)/1 – sin² A

= 1 + sin A/cos² A

= 1 + sin A/cos A

= 1/cos A + sin A/cos A

= sec A + tan A

= R.H.S

(vii) (sin θ – 2sin³θ)/(2cos³θ-cos θ) = tan θ

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7+tan²A+cot²A

(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)

 [Hint : Simplify LHS and RHS separately]

(x) (1+tan²A/1+cot²A) = (1-tan A/1-cot A)² = tan²A

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2