Solve the followings Questions.

1. In Δ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :
(i) sin A, cos A
(ii) sin C, cos C

Answer:

Let us draw a right angled triangle ABC, right angled at B.

Using Pythagoras theorem,

(i) 

(ii)

, 

2. In adjoining figure, find tan P – cot R.

Answer:

3. If sin A =3/4, calculate cos A and tan A.

Answer:

Given: A triangle ABC in which

B =90

We know that sin A = BC/AC = 3/4
Let BC be 3k and AC will be 4k where k is a positive real number.
By Pythagoras theorem we get,
AC² = AB² + BC²
(4k)² = AB² + (3k)²
16k² – 9k² = AB²
AB² = 7k²
AB = √7 k
cos A = AB/AC = √7 k/4k = √7/4
tan A = BC/AB = 3k/√7 k = 3/√7

4. Given 15 cot A = 8, find sin A and sec A.

Answer:

Let ΔABC be a right-angled triangle, right-angled at B.
We know that cot A = AB/BC = 8/15   (Given)
Let AB be 8k and BC will be 15k where k is a positive real number.
By Pythagoras theorem we get,
AC² = AB² + BC²
AC² = (8k)² + (15k)²
AC² = 64k² + 225k²
AC² = 289k²
AC = 17 k
sin A = BC/AC = 15k/17k = 15/17
sec A = AC/AB = 17k/8 k = 17/8

5. Given sec θ = 13/12, calculate all other trigonometric ratios.

Answer:

Consider a triangle ABC in which

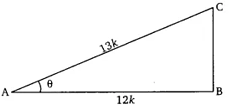
Let AB = 12k and AC = 13k

Then, using Pythagoras theorem,

(AC)2 = (AB)2 + (BC)2

(13 k)2 = (12 k)2 + (BC)2

169 k2 = 144 k2 + BC2

25 k2 = BC2

BC = 5 k

 (I)   Sin  = 

=  = 

(ii) Cos θ = 

=   = 

(iii)Tan θ = 

=  = 

(iv) Cot θ = 

=  = 

(v) Cosec θ = 

=  = 

6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Answer:

cosA=cos

But 

7. If cot θ =7/8, evaluate :
(i)(1+sin θ )(1-sin θ)/(1+cos θ)(1-cos θ)
(ii) cot²θ

Answer:

Consider a triangle ABC 

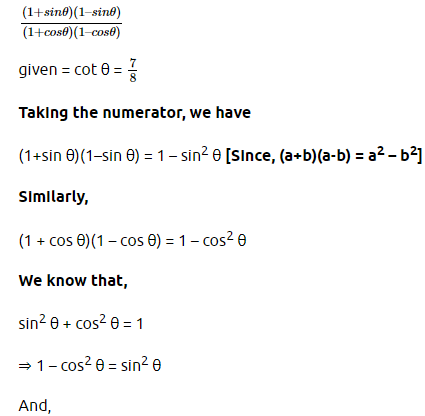
 (ii)

8. If 3cot A = 4/3 , check whether (1-tan²A)/(1+tan²A) = cos²A – sin²A or not.

Answer:

Consider a triangle ABC AB=4cm, BC= 3cm

.

And 

9. In triangle ABC, right-angled at B, if tan A =1/√3 find the value of:

(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C

Answer:

Consider a triangle ABC in which

.

(i) 

(ii) 

10. In Δ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.

Answer:

Given that, PR + QR = 25 , PQ = 5
Let PR be x.  ∴ QR = 25 – x
By Pythagoras theorem ,
PR2 = PQ² + QR²
x² = (5)2 + (25 – x)²
x² = 25 + 625 + x² – 50x
50x = 650
x = 13
∴ PR = 13 cm
QR = (25 – 13) cm = 12 cm
sin P = QR/PR = 12/13
cos P = PQ/PR = 5/13
tan P = QR/PQ = 12/5

11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 4/3 for some angle θ.

Answer:

i) False.
In ΔABC in which ∠B = 90º,
     AB = 3, BC = 4 and AC = 5
Value of tan A = 4/3 which is greater than.
The triangle can be formed with sides equal to 3, 4 and hypotenuse = 5 as
it will follow the Pythagoras theorem.
AC² = AB² + BC²
5² = 3² + 4²
25 = 9 + 16
25 = 25

(ii) True.
Let a ΔABC in which ∠B = 90º,AC be 12k and AB be 5k, where k is a positive real number.
By Pythagoras theorem we get,
AC² = AB² + BC²
(12k)² = (5k)² + BC²
BC² + 25k² = 144k²
BC² = 119k²
Such a triangle is possible as it will follow the Pythagoras theorem.

(iii) False.
Abbreviation used for cosecant of angle A is cosec A.cos A is the abbreviation used for cosine of angle A.

(iv) False.
cot A is not the product of cot and A. It is the cotangent of ∠A.

(v) False.
sin θ = Height/Hypotenuse
We know that in a right angled triangle, Hypotenuse is the longest side.
∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2