Solve the followings Questions.

1. Determine t]“1he ratio in which the line 2x + y -4 =0 divides the line segment joining the points A(2,-2) and B(3,7).

Answer:

Let the given line divide the line segment joining the points A(2, −2) and B(3, 7) in a ratio k : 1

Coordinates of the point of division =

This point also lies on 2x + y – 4 = 0

⇒

⇒

⇒  9k – 2 = 0

⇒  k = 2/9

Therefore, the ratio in which the line 2x + y – 4 = 0  divides the line segment joining the points A(2, −2) and B(3, 7) is 2:9.

2. Find a relation between x and y if the points (x,y),(1, 2)and (7, 0)are collinear.

Answer:

If the given points are collinear, then the area of triangle formed by these points will be 0.

Area of triangle = 

 Area = 

0 = 1/2 [2x – y + 7y – 14]

0 =1/2 [2x + 6y – 14]

[2x + 6y – 14] = 0

x + 3y – 7 = 0

This is the required relation between x & y.

3. Find the centre of a circle passing through the points (6,-6), B(3,-7)and (3, 3).

Answer:

 Let O (x,y) be the centre of the circle. And let the points (6, −6), (3, −7), and (3, 3) be representing the points A, B, and C on the circumference of the circle.

However OA = OB (Radii of same circle)

⇒ 

=>x² + 36 – 12x + y² + 36 + 12y = x² + 9 – 6x + y² + 49 -14y

⇒ -6x + 2y + 14 = 0

⇒ 3x + y = 7 ….1

Similary OA = OC (Radii of same circle)

=>x² + 36 – 12x + y² + 36 + 12y = x² + 9 – 6x + y² + 9 – 6y

⇒ -6x + 18y + 54 = 0

⇒ -3x + 9y = -27  …..(2)

On adding equation (1) and (2), we obtain

10y = – 20

y = – 2

From equation (1), we obtain

3x − 2 = 7

3x = 9

x = 3

Therefore, the centre of the circle is (3, −2).

4. The two opposite vertices of a square are (-1,2) and (3,2). Find the coordinates of the other two vertices.

Answer

Let ABCD be a square having (−1, 2) and (3, 2) as vertices A and C respectively. Let (x,y), (x₁,y₁) be the coordinate of vertex B and D respectively.

We know that the sides of a square are equal to each other.

∴ AB = BC

=>x² + 2x + 1 + y²  -4y + 4 = x² + 9  -6x + y² + 4 – 4y

⇒ 8x = 8

⇒ x = 1

We know that in a square, all interior angles are of 90°.

In ΔABC,

AB² + BC² = AC²

⇒4 + y² + 4 − 4y + 4 + y² + 4 − 4y = 16

⇒2y² + 16 − 8 = 16

⇒2y² – 8 = 0

⇒y(y – 4) = 0

⇒y = 0 or 4

We know that in a square, the diagonals are of equal length and bisect each other at 90°. Let O be the mid-point of AC. Therefore, it will also be the mid-point of BD

Coordinate of point O = ((-1+3)/2, (2+2)/2)

⇒1 + x1/2 = 1

⇒1 + x1 = 2

⇒x1 = 1

and y + y_{1 /2 = 2}

⇒ y + y1= 4

⇒If y = 0

⇒y1= 4

⇒If y = 4

⇒y1= 0

Therefore, the required coordinates are (1, 0) and (1, 4).

5. The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

(i) Taking A as origin, find the coordinates of the vertices of the triangle.

(ii) What will be the coordinates of the vertices of △ PQR if C is the origin? Also calculate the area of the triangle in these cases. What do you observe?

Answer:

(i) Taking A as the origin, AD and AB as the coordinate axes. Clearly, the points P, Q and

R are (4, 6), (3, 2) and (6, 5) respectively.

(ii)Taking C as the origin, CB and CD as the coordinate axes. Clearly, the points P, Q and R are given by (12, 2), (13, 6) and (10, 3) respectively.

We know that the area of the triangle (POR) =

= 1/2 [4(2-5) + 3(5-6) + 6(6-2)]

= 1/2 [-12 -3 +24]

= 9/2 sq. units

(ii) Taking C as origin, CB as x- axis, and CD as y- axis, the coordinates of vertices P, Q, and R are (12, 2), (13, 6), and (10, 3) respectively.

area of the triangle (PQR) =

= 1/2[12(6-3) + 13(3-2) + 10(2-6)

= 1/2 [36+13-40]

= 9/2 sq. units

Hence, the areas are same in both the cases.

6. The vertices of a △ ABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that AD/AB = AE/AC = 1/4 .Calculate the area of the △ ADE and compare it with the area of △ ABC.

Answer:

Given that (AD)/(AB) = (AE)/(AC) = 1/4

(AD)/(AD+DB) = (AE)/(AE+EC) = 1/4

(AD)/(DB)=(AE)/(EC) = 1/3

Therefore, D and E are two points on side AB and AC respectively such that they divide side AB and AC in a ratio of 1:3

Coordinates of Point D == (13/4, 23/4)

Coordinates of Point E = = (19/4, 20/4)

Area of triangle =

Area of ΔADE =

 =

Area of ΔABC = 1/2[4(5-2) + 1(2-6) + 7(6-5)]

= 1/2[12 – 4 + 7]

= 15/2

Clearly, the ratio between the areas of ΔADE and ΔABC is 1:16.

7. Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of △ ABC.

(i) The median from A meets BC at D. Find the coordinates of the point D.

(ii) Find the coordinates of the point P on AD such that AP: PD = 2: 1.

(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ: QE = 2: 1 and CR : RF = 2 : 1.

(iv) What do you observe?

(Note: The point which is common to all the three medians is calledcentroid and this point divides each median in the ratio 2: 1)

(v) If A(x₁,y₁), B(x₂,y₂),and C(x₃,y₃),are the vertices of △ ABC, find the coordinates of the centroid of the triangle.

Answer:

(i) Median AD of the triangle will divide the side BC in two equal parts.

Therefore, D is the mid-point of side BC

Coordinate of D = (6 +1/2, 5 + 4/2) =(7/2,9/2)

(ii) Point P divides the side AD in a ratio 2:1.

Coordinate of P = = (11/3 , 11/3)

(iii) Median BE of the triangle will divide the side AC in two equal parts.

Therefore, E is the mid-point of side AC.

Coordinate of E = (4+1/2, 2+4/2) = (5/2,3)

Point Q divides the side BE in a ratio 2:1.

Coordinate of Q =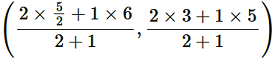= (11/3 , 11/3)

Median CF of the triangle will divide the side AB in two equal parts. Therefore, F is the mid-point of side AB

Coordinate of F = (4+6/2, 2+5/2) = (5,7/2)

Point R divides the side CF in a ratio 2:1.

Coordinate of R =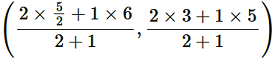= (11/3 , 11/3)

(iv) It can be observed that the coordinates of point P, Q, R are the same.

Therefore, all these are representing the same point on the plane i.e., the centroid of the triangle.

(v) Consider a triangle, ΔABC, having its vertices as A(x₁,y₁), B(x₂,y₂) and C(x₃,y₃)

Median AD of the triangle will divide the side BC in two equal parts. Therefore, D is the mid-point of side BC.

Coordinate of D =

Let the centroid of this triangle be O.

Point O divides the side AD in a ratio 2:1.

Coordinate of O =

= 

8. ABCD is a rectangle formed by joining points A(-1,-1), B (-1,4), C (5,4) and D (5,-1). P, Q, R and S are the mid-points of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? Or a rhombus? Justify your answer.

Answer:

P is the mid point of side AB

Therefore the coordinates of P are ((-1-1)/2,(-1+4)/2) = (-1, 3/2)

Similary the coordinates of Q , R and S are  (2,4),(5, 3/2), and (2, -1) respectilvely

Length of PQ =

Length of QR =

Length of RS =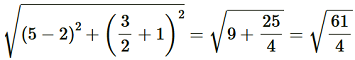

Length of SP =

Length of PR == 6

Length of QS == 5

It can be observed that all sides of the given quadrilateral are of the same measure. However, the diagonals are of different lengths. Therefore, PQRS is a rhombus.

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2