Solve the followings Questions.

1. Find the distance between the following pairs of points:

(i) (2, 3), (4,1)

(ii) (–5, 7), (–1, 3)

(iii) (a, b), (–a, –b)

Answer:

(i) Distance between the points is given by

Therefore the distance between (2,3) and (4,1) is given by

l =

=

= √4+4 = √8 = 2√2

(ii)Applying Distance Formula to find distance between points (–5, 7) and (–1, 3), we get

l =

 =

 = √16+16 = √32 = 4√2

(iii)Applying Distance Formula to find distance between points (a, b) and (–a, –b), we get

l =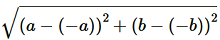

=

=

2. Find the distance between the points (0, 0) and (36, 15). Also, find the distance between towns A and B if town B is located at 36 km east and15 km north of town A.

Answer:

Applying Distance Formula to find distance between points (0, 0) and (36, 15), we get

=

= √1296 + 225 = √1521 = 39

Yes, we can find the distance between the given towns A and B.

Assume town A at origin point (0, 0).

Therefore, town B will be at point (36, 15) with respect to town A.

And hence, as calculated above, the distance between town A and B will be 39km.

3. Determine if the points (1, 5), (2, 3) and (–2, –11) are collinear.

Answer:

Let A = (1, 5), B = (2, 3) and C = (–2, –11)

Using Distance Formula to find distance AB, BC and CA.

BC =

CA =

Since AB+BC ≠ CA

Therefore, the points (1, 5), (2, 3), and (−2, −11) are not collinear.

4. Check whether (5, –2), (6, 4) and (7, –2) are the vertices of an isosceles triangle.

Answer:

Let A = (5, –2), B = (6, 4) and C = (7, –2)

Using Distance Formula to find distances AB, BC and CA.

AB =

BC =

CA =

Since AB = BC.

Therefore, A, B and C are vertices of an isosceles triangle.

5. In a classroom, 4 friends are seated at the points A (3, 4), B (6, 7), C (9, 4) and D (6, 1). Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli. “Don’t you think ABCD is a square?”Chameli disagrees. Using distance formula, find which of them is correct.

Answer:

We have A = (3, 4), B = (6, 7), C = (9, 4) and D = (6, 1)

Using Distance Formula to find distances AB, BC, CD and DA, we get

AB =

BC =

CD =

AD =

Therefore, All the sides of ABCD are equal here

Now, we will check the length of its diagonals.

AC =

BD =

So, Diagonals of ABCD are also equal.

we can definitely say that ABCD is a square.

Therefore, Champa is correct.

6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.

(i) (–1, –2), (1, 0), (–1, 2), (–3, 0)

(ii) (–3, 5), (3, 1), (0, 3), (–1, –4)

(iii) (4, 5), (7, 6), (4, 3), (1, 2)

Answer:

(i)Let A = (–1, –2), B = (1, 0), C= (–1, 2) and D = (–3, 0)

Using Distance Formula to find distances AB, BC, CD and DA, we get

AB =

BC =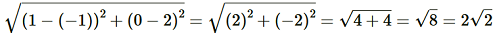

CD =

AD =

Therefore, all four sides of quadrilateral are equal.

Now, we will check the length of diagonals.

AC =

BD =

Therefore, diagonals of quadrilateral ABCD are also equal.

we can say that ABCD is a square.

(ii)Let A = (–3, 5), B= (3, 1), C= (0, 3) and D= (–1, –4)

Using Distance Formula to find distances AB, BC, CD and DA, we get

AB =

BC =

CD =

DA =

We cannot find any relation between the lengths of different sides.

Therefore, we cannot give any name to the quadrilateral ABCD.

(iii)Let A = (4, 5), B= (7, 6), C= (4, 3) and D= (1, 2)

Using Distance Formula to find distances AB, BC, CD and DA, we get

AB =

BC =

CD =

DA =

Here opposite sides of quadrilateral ABCD are equal.

We can now find out the lengths of diagonals.

AC =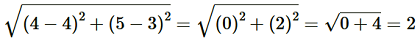

BD =

Here diagonals of ABCD are not equal.

 we can say that ABCD is not a rectangle therefore it is a parallelogram.

7. Find the point on the x–axis which is equidistant from (2, –5) and (–2, 9).

Answer:

Let the point be (x, 0) on x–axis which is equidistant from (2, –5) and (–2, 9).

Using Distance Formula and according to given conditions we have:

⇒

Squaring both sides, we get

⇒

(x-2)² + 25 = (x+2)² + 81

x² + 4 – 4x + 25 = x² + 4 + 4x + 81

8x = – 25 – 81

8x = -56

x = – 7

Therefore, point on the x–axis which is equidistant from (2, –5) and (–2, 9) is (–7, 0)

8. Find the values of y for which the distance between the points P (2, –3) and Q (10, y) is 10 units.

Answer:

Using Distance formula, we have

⇒

⇒ 64 + (y +3)² = 100

⇒ (y+3)² = 100-64 = 36

⇒ y+3 = ± 6

⇒ y+3=6 or y+3 = – 6

Therefore y = 3 or -9

9. If, Q (0, 1) is equidistant from P (5, –3) and R (x, 6), find the values of x. Also, find the distances QR and PR.

Answer:

It is given that Q is equidistant from P and R. Using Distance Formula, we get

PQ = RQ

⇒√25+16 = √x² + 25

⇒41 = x² + 25

 16 = x²

 x = ± 4

Thus, R is (4, 6) or (–4, 6).

When point R is (4,6)

 PR =

 QR =

When point R is (- 4,6)

PR = 

 QR =

10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (–3, 4).

Answer:

It is given that (x, y) is equidistant from (3, 6) and (–3, 4).

Using Distance formula, we can write

⇒

⇒ (x-3)² + (y-6)² = (x+3)² + (y-4)²

⇒ x² + 9 -6x + y² + 36 – 12y = x² + 9 + 6x + y² + 16 – 8y

⇒36- 16 = 6x + 6x + 12y  – 8y

⇒20 = 12x + 4y

⇒3x + y = 5

⇒3x + y – 5 = 0

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2