Solve the followings Questions.

1. Sides of triangles are given below. Determine which of them are right triangles? In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm

Answer:
(i) Given that the sides of the triangle are 7 cm, 24 cm, and 25 cm.
Squaring the lengths of these sides, we will get 49, 576, and 625.
49 + 576 = 625
(7)² + (24)² = (25)²
The sides of the given triangle are satisfying Pythagoras theorem.Hence, it is right angled triangle.
Length of Hypotenuse = 25 cm

(ii) Given that the sides of the triangle are 3 cm, 8 cm, and 6 cm.
Squaring the lengths of these sides, we will get 9, 64, and 36.
However, 9 + 36 ≠ 64
Or, 3² + 6² ≠ 8²
Clearly, the sum of the squares of the lengths of two sides is not equal to the square of the length of the third side.
Therefore, the given triangle is not satisfying Pythagoras theorem.

(iii) Given that sides are 50 cm, 80 cm, and 100 cm.
Squaring the lengths of these sides, we will get 2500, 6400, and 10000.
However, 2500 + 6400 ≠ 10000
Or, 50² + 80² ≠ 100²
Clearly, the sum of the squares of the lengths of two sides is not equal to the square of the length of the third side.
Therefore, the given triangle is not satisfying Pythagoras theorem.
Hence, it is not a right triangle.

(iv) Given that sides are 13 cm, 12 cm, and 5 cm.
Squaring the lengths of these sides, we will get 169, 144, and 25.
Clearly, 144 +25 = 169
Or, 12² + 5² = 13²
The sides of the given triangle are satisfying Pythagoras theorem.
Therefore, it is a right triangle.
Length of the hypotenuse of this triangle is 13 cm.

2. PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM × MR.

Answer:

Given: ΔPQR is right angled at P is a point on QR such that PM ⊥QR.
To prove:. PM² = QM × MR
Proof: In ΔPQM, we have
PQ² = PM² + QM² [By Pythagoras theorem]
Or, PM² = PQ² – QM² …(i)
In ΔPMR, we have
PR² = PM² + MR² [By Pythagoras theorem]
Or, PM² = PR² – MR² …(ii)
Adding (i) and (ii), we get
2PM² = (PQ² + PM2) – (QM² + MR²)
= QR² – QM² – MR²        [∴ QR² = PQ² + PR²]
= (QM + MR)² – QM² – MR²
= 2QM × MR
∴ PM² = QM × MR

3. In figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB² = BC × BD
(ii) AC² = BC × DC
(iii) AD² = BD × CD

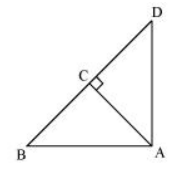
Answer:

Given: ABD is a triangle right angled at A and AC ⊥ BD.

(i) In ΔADB and ΔCAB, we have

∠DAB = ∠ACB (Each equals to 90°)

∠ABD = ∠CBA (Common angle)

∴ ΔADB ~ ΔCAB [AA similarity criterion]

⇒  AB/CB = BD/AB

⇒  AB² = CB × BD

(ii) Let ∠CAB = x

In ΔCBA,

∠CBA = 180° – 90° – x

∠CBA = 90° – x

Similarly, in ΔCAD

∠CAD = 90° – ∠CBA

= 90° – x

∠CDA = 180° – 90° – (90° – x)

∠CDA = x

In ΔCBA and ΔCAD, we have

∠CBA = ∠CAD

∠CAB = ∠CDA

∠ACB = ∠DCA (Each equals to 90°)

∴ ΔCBA ~ ΔCAD [By AAA similarity criterion]

⇒ AC/DC = BC/AC

⇒  AC² = DC × BC

(iii) In ΔDCA and ΔDAB, we have

∠DCA = ∠DAB (Each equals to 90°)

∠CDA = ∠ADB (common angle)

∴ ΔDCA ~ ΔDAB [By AA similarity criterion]

⇒ DC/DA = DA/DA

 ⇒ AD² = BD × CD

4. ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².

Answer:

Since ABC is an isosceles right triangle, right angled at C.

∴ AC = CB

Applying Pythagoras theorem in ΔABC (i.e., right-angled at point C), we obtain

AC² + CB² = AB²

⇒ AC² +  AC² = AB² ( AC = CB)

⇒ 2 AC² = AB²

5. ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ABC is a right triangle.

Answer:

Given that ΔABC is an isosceles triangle having AC = BC and AB² = 2AC²
In ΔACB,
AC = BC (Given)
AB² = 2AC² (Given)
AB2 = AC² + AC²
= AC² + BC² [Since, AC = BC]
Hence, By Pythagoras theorem ΔABC is right angle triangle.

6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.

Answer:

 ABC is an equilateral triangle of side 2a.
Draw, AD ⊥ BC
In ΔADB and ΔADC, we have
AB = AC [Given]
AD = AD [Given]
∠ADB = ∠ADC [equal to 90°]
Therefore, ΔADB ≅ ΔADC by RHS congruence.
Hence, BD = DC [by CPCT]
In right angled ΔADB,
AB² = AD² + BD²
(2a)² = AD² + a²
⇒ AD²  = 4a² – a²
⇒ AD²  = 3a²
⇒ AD  = √3a

7. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of squares of its diagonals.

Answer:

Let the diagonals AC and BD of rhombus ABCD intersect each other at O. Since the diagonals of a rhombus bisect each other at right angles.

In ΔAOB, ΔBOC, ΔCOD, ΔAOD,

Applying Pythagoras theorem, we obtain

AB² = AO² + OB² ….(1)

BC² = BO² + OC² …. (2)

CD² = CO² + OD² …..(3)

AD² = AO² + OD² ……(4)

Adding all  these equation we obtain

AB² + BC² + CD² + AD² = 2(AO² + OB² + OC² + OD²)

=

(Diagonals bisect each other)

 =

 = (AC)² + (BD)²

8. In Fig. O is a point in the interior of a triangle
ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE² ,
(ii) AF² + BD² + CE² = AE² + CD² + BF².
 

Answer:

 Applying Pythagoras theorem in ΔAOF, we obtain

OA² = OF² + AF²

Similarly, in ΔBOD

OB² = OD² + BD²

Similarly, in ΔCOE

OC² = OE² + EC²

Adding these equations,

OA² + OB² + OC² = OF² + AF² + OD² + BD² + OE² + EC²

OA² + OB² + OC² – OF² – OD² – OE² = AF² + BD² + EC²

From above result

AF² + BD² + EC² = (OA²- OE² ) + (OC² – OD²) + (OB² – OF² )

∴ AF² + BD² + EC² = AE² + CD² + BF².

9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.

Answer:

Let OA be the wall and AB be the ladder.

Therefore, by Pythagoras theorem,

AB² = OA² + BO²

(10 m)² =( 8 m)² + OB²

100m² = 64m² + OB²

OB² = 36m²

OB = 6m

Therefore the distance of the foot of the ladder from the base of the wall is 6 m.

10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other hand. How far from the base of the pole should the stake be driven so that the wire will be taut?

Answer:

Let AB (= 24m) be a guy wire attached to a vertical pole. BC of height 18 m. To keep the wire taut, let it be fixed to a stake at A. Then, ABC is a right triangle, right angled at O.

Let OB be the pole and AB be the wire.

By Pythagoras theorem,

AB² = OB² + OA²

(24 m)² = ( 18 m)² + OA²

576m² = 324m² + OA²

OA² = (576 – 324)m² = 25m²

OA² = √252 m = √6 x 6 x 7 = 6√7 m.

OA =6√7 m.

Hence, the stake may be placed at distance of 6√7 m from the base of the pole.

11. An aeroplane leaves an airport and flies due north at a speed of 1000 km pwe hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after hours?

Answer:

Let the first aeroplane starts from O and goes upto A towards north where

Distance travelled by the plane flying towards north in  hrs

Similarly, distance travelled by the plane flying towards west inhrs

Let these distances be represented by OA and OB respectively.

Applying Pythagoras theorem,

Distance between these planes after

 = √[(1500)² + (1800)²]

= √(5490000)

Therefore, the distance between these planes will be 300√61 km.

12. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.

Answer:

Let CD and AB be the poles of height 11 m and 6 m.

Therefore, CP = 11 − 6 = 5 m.

From the figure, it can be observed that AP = 12m

Applying Pythagoras theorem for ΔAPC, we obtain

AP² + PC² = AC²

(12m)² + (5m)² = AC²

AC² = (144 + 25)m² = 169m²

AC = 13m

Therefore, the distance between their tops is 13 m.

13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².

Answer:

 Applying Pythagoras theorem in ΔACE, we get
AC² + CE² = AE² ….(i)
Applying Pythagoras theorem in ΔBCD, we get
BC² + CD² = BD² ….(ii)
Using equations (i) and (ii), we get
AC² + CE² + BC² + CD² = AE² + BD² …(iii)
Applying Pythagoras theorem in ΔCDE, we get
DE² = CD² + CE²
Applying Pythagoras theorem in ΔABC, we get
AB² = AC² + CB²
Putting these values in equation (iii), we get
DE² + AB² = AE² + BD².

14. The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD (see Fig.). Prove that 2AB² = 2AC² + BC².

Answer:

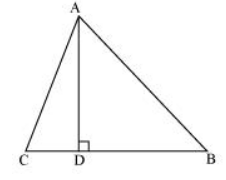
Given that in ΔABC, we have
AD ⊥BC and BD = 3CD
In right angle triangles ADB and ADC, we have
AB² = AD² + BD² …(i)
AC² = AD² + DC² …(ii) [By Pythagoras theorem]
Subtracting equation (ii) from equation (i), we get
AB² – AC² = BD² – DC²
= 9CD² – CD²  [∴ BD = 3CD]               
= 9CD² = 8(BC/4)² [Since, BC = DB + CD = 3CD + CD = 4CD]
Therefore, AB² – AC² = BC²/2
⇒ 2(AB² – AC²) = BC²
⇒ 2AB² – 2AC² = BC²
∴ 2AB² = 2AC² + BC².

15. In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3BC. Prove that 9AD² = 7AB².

Answer:

Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.

∴ BE = EC = BC/2 = a/2

and AE= a√3/2

Given that, BD = 1/3 BC

∴ BD = a/3

DE = BE – BD = a/2 – a/3 = a/6

Applying Pythagoras theorem in ΔADE, we get

AD² = AE² + DE²

AD² = (a√3/2)² + (a/6)²

AD² = (3a²/4) + (a²/36)

 ⇒ AD² = (28a²/36)

 ⇒ AD² = 7/9AB²

⇒ 9AD² = 7AB²

16. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.

Answer:

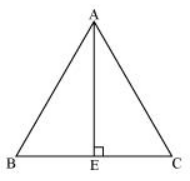
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.

∴ BE = EC = BC/2 = a/2

Applying Pythagoras theorem in ΔABE, we obtain

AB² = AE² + BE²

a² = AE² + (a/2)²

AE² = a² – a²/4

 AE²  = 3a²/4

4 AE² = 3a²

⇒ 4 × (Square of altitude) = 3 × (Square of one side).

17. Tick the correct answer and justify: In ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm.
The angle B is:
(A) 120°
(B) 60°
(C) 90°
(D) 45°

Answer:

Given that, AB = 6√3 cm, AC = 12 cm, and BC = 6 cm
We can observe that
AB² = 108
AC² = 144
And, BC² = 36
AB² + BC² = AC²
The given triangle, ΔABC, is satisfying Pythagoras theorem.
Therefore, the triangle is a right triangle, right-angled at B.
∴ ∠B = 90°
Hence, the correct option is (C).
 

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2