Solve the followings Questions.

1. Let ΔABC ~ ΔDEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.

Answer:

It is given that,
Area of ΔABC = 64 cm²
Area of ΔDEF = 121 cm²
EF = 15.4 cm
and, ΔABC ~ ΔDEF
∴ Area of ΔABC/Area of ΔDEF = AB²/DE²
= AC2/DF² = BC²/EF² …(i)
[If two triangles are similar, ratio of their areas are equal to the square of the ratio of their corresponding sides]
∴ 64/121 = BC²/EF²
⇒ (8/11)² = (BC/15.4)²
⇒ 8/11 = BC/15.4
⇒ BC = 8×15.4/11
⇒ BC = 8 × 1.4
⇒ BC = 11.2 cm

2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.

Answer:

ABCD is a trapezium with AB || DC. Diagonals AC and BD intersect each other at point O.
In ΔAOB and ΔCOD, we have
∠1 = ∠2 (Alternate angles)
∠3 = ∠4 (Alternate angles)
∠5 = ∠6 (Vertically opposite angle)
∴ ΔAOB ~ ΔCOD [By AAA similarity criterion]
Now, Area of (ΔAOB)/Area of (ΔCOD)
= AB²/CD² [If two triangles are similar then the ratio of their areas are equal to the square of the ratio of their corresponding sides]
= (2CD)²/CD² [∴ AB = CD]
∴ Area of (ΔAOB)/Area of (ΔCOD)
= 4CD²/CD = 4/1
Hence, the required ratio of the area of ΔAOB and ΔCOD = 4:1

3. In figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that area (ΔABC)/area (ΔDBC) = AO/DO.

Answer:

Let us draw two perpendiculars AP and DM on line BC.

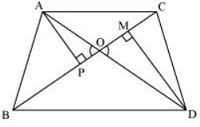
We know that area of a triangle = 1/2 x Base x Height

 ∴  

In ΔAPO and ΔDMO,

∠APO = ∠DMO (Each = 90°)

∠AOP = ∠DOM (Vertically opposite angles)

∴ ΔAPO ∼ ΔDMO (By AA similarity criterion)

∴  AP/DM = AO/DO

⇒ 

4. If the areas of two similar triangles are equal, prove that they are congruent.

Answer:

Let us assume two similar triangle as ΔABC ~ ΔPQR

Given that, ar(ΔABC) = ar(ΔABC)

Putting this value in equation (1) we obtain

 1 = 

 ⇒  AB = PQ, BC = QR and AC = PR

∴  ΔABC ≅ ΔPQR   (By SSS congruence criterion)

5. D, E and F are respectively the mid-points of sides AB, BC and CA of Δ ABC. Find the ratio of the areas of Δ DEF and Δ ABC.

Answer:

D and E are the mid-points of ΔABC

:.DE || AC and DE = 1/2 AC

In ΔBED and ΔBCA 

∠BED = ∠BCA   (Corresponding angle)

∠BDE = ∠BAC   (Corresponding angle)

∠EBD = ∠CBA   (Common angles)

∴ΔBED ~ ΔBCA (AAA similarity criterion)

⇒

Similary

⇒

Also ar(ΔDEF) = ar(ΔABC) –  [ar(ΔBED) + ar(ΔCFE) + ar(ΔADF)]

⇒

⇒

6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Answer:

Let us assume two similar triangles as ΔABC ∼ ΔPQR. Let AD and PS be the medians of these triangles.

∵  ΔABC ∼ ΔPQR

:.(AB)/(PQ) = (BC)/(QR) = (AC)/(PR)…(1)

∠A = ∠P, ∠B = ∠Q, ∠C = ∠R … (2)

Since AD and PS are medians,

∴ BD = DC = BC/2

And, QS = SR = QR/2

Equation (1) becomes

(AB)/(PQ) = (BD)/(QS) = (AC)/(PR)  ….(3)

In ΔABD and ΔPQS,

∠B = ∠Q [Using equation (2)]

and (AB)/(PQ) = (BD)/(QS)    [Using equation (3)]

∴ ΔABD ∼ ΔPQS (SAS similarity criterion)

Therefore, it can be said that

AB/PQ = BD/QS = AD/PS ….(4)

From equations (1) and (4), we may find that

AB/PQ = BC/QR = AC/PR = AD/PS

And hence,

7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of the diagonals.
Tick the correct answer and justify:

Answer:

Let ABCD be a square of side a.

Therefore, its diagonal = √2a

Two desired equilateral triangles are formed as ΔABE and ΔDBF.

Side of an equilateral triangle, ΔABE, described on one of its sides = a

Side of an equilateral triangle, ΔDBF, described on one of its diagonals =√2a

We know that equilateral triangles have all its angles as 60º and all its sides of the same length. Therefore, all equilateral triangles are similar to each other. Hence, the ratio between the areas of these triangles will be equal to the square of the ratio between the sides of these triangles.

8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is:

(A) 2: 1

(B) 1: 2

(C) 4: 1

(D) 1: 4

Answer:

We know that equilateral triangles have all its angles as 60º and all its sides of the same length. Therefore, all equilateral triangles are similar to each other. Hence, the ratio between the areas of these triangles will be equal to the square of the ratio between the sides of these triangles.

Let side of ΔABC = x

Therefore, side of  ΔBDE = x/2

Hence, (C) is the correct answer.

9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio:

(A) 2: 3

(B) 4: 9

(C) 81: 16

(D) 16: 81

Answer:

If two triangles are similar to each other, then the ratio of the areas of these triangles will be equal to the square of the ratio of the corresponding sides of these triangles.

It is given that the sides are in the ratio 4:9.

Therefore, ratio between areas of these triangles = (4/9)² = 16/81

Hence,(D) is the correct answer.

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2