Solve the followings Questions.

1. In figure (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

Answer:

(i) Since DE || BC,

Let, EC = x cm

It is given that DE || BC

By using basic proportionality theorem, we obtain

x = 2

EC = 2 cm.

(ii) Let AD = x cm.

It is given that DE || BC.

By using basic proportionality theorem, we obtain

x = 2.4

AD = 2.4cm.

2. E and F are points on the sides PQ and PR respectively of a ∆ PQR. For each of the following cases, state whether EF II QR:

(i) PE = 3.9 cm, EQ = 3cm, PF = 3.6 cm and FR = 2.4 cm

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

Answer:

(i)Given: PE = 3.9 cm, EQ = 3cm, PF = 3.6 cm and FR = 2.4 cm

Hence,

Therefore, EF is not parallel to QR.

(ii)Given: PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

Therefore,EF is parallel to QR.

(iii)Given: PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

And ER = PR – PF = 2.56 – 0.36 = 2.20 cm

Hence,

Therefore, EF is parallel to QR.

3. In figure, if LM || CB and LN || CD, prove that AM/AB = AN/AD.

Answer:

In figure, LM || CB

By using Basic Proportionality theorem

And in ∆ ACD, LN || CD

  ……i

Similalry, in ∆ ACD, LN || CD

  …….ii

By using Basic Proportionality theorem

From eq. (i) and (ii), we have

4. In figure, DE || AC and DF || AE. Prove that BF/GE = BE/EC .

Answer:

In ∆ BCA, DE || AC

[Basic Proportionality theorem] ……….(i)

And in ∆ BEA, DF || AE

[Basic Proportionality theorem] ……….(ii)

From eq. (i) and (ii), we have

5. In figure, DE || OQ and DF || OR. Show that EF || QR.

Answer:

In ∆ PQO, DE || OQ

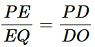[Basic Proportionality theorem] ……….(i)

And in ∆ POR, DF || OR

[Basic Proportionality theorem] ……….(ii)

From eq. (i) and (ii), we have

Therefore, EF || QR [By the converse of Basic Proportionality Theorem]

6. In figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Answer:

And in ∆ POQ, AB || PQ

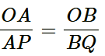[Basic Proportionality theorem] ……….(i)

And in ∆ OPR, AC || PR

[Basic Proportionality theorem] ……….(ii)

From eq. (i) and (ii), we have

Therefore, BC || QR (By the converse of Basic Proportionality Theorem)

7. Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).

Answer:

Consider the given figure in which l  is a line  drawn through the mid-point P of line segment AB meeting AC at Q, such that  PQ || BC

 By using Basic Proportionality theorem, we obtain,

    (P is the midpoint of AB ∴ AP = PB)

⇒ AQ = QC

Or, Q is the mid-point of AC.

8. Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).

Answer:

Given: A triangle ABC, in which P and Q are the mid-points of

sides AB and AC respectively.

Consider the given figure in which PQ is a line segment joining the mid-points P and Q of line AB and AC respectively.

i.e., AP = PB and AQ = QC

It can be observed that

and 

 Therefore, 

Hence, by using basic proportionality theorem, we obtain

PQ || BC.

9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AO/BO = CO/DO .

Answer:

Given: A trapezium ABCD, in which AB || DC and its diagonals

AC and BD intersect each other at O.

Draw a line EF through point O, such that EF || CD

In ΔADC, EO || CD

By using basic proportionality theorem, we obtain

   …i

In ΔABD, OE || AB

So, by using basic proportionality theorem, we obtain

⇒   …ii

From eq. (i) and (ii), we get

⇒

10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO = CO/DO Such that ABCD is a trapezium.

Answer:

Given: A quadrilateral ABCD, in which its diagonals AC and

BD intersect each other at O such that , i.e.

Quadrilateral ABCD is a trapezium.

Construction: Through O, draw OE || AB meeting AD at E.

In ∆ ADB, we have OE || AB [By construction] By Basic Proportionality theorem

 …..i

However, it is given that

 …..ii

From eq. (i) and (ii), we get

⇒ EO || DC [By the converse of basic proportionality theorem]

⇒ AB || OE || DC

⇒ AB || CD

∴ ABCD is a trapezium.

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2