1. Solve the following pairs of equations by reducing them to a pair of linear equations:

(i) 1/2x + 1/3y = 2
1/3x + 1/2y = 13/6

(ii) 2/√x +3/√y = 2
4/√x – 9/√y = -1

(iii) 4/x + 3y = 14
3/x – 4y = 23

(iv) 5/x-1 + 1/y-2 = 2
6/x-1 – 3/y-2 = 1

(v) 7x-2y/xy = 5
8x + 7y/xy = 15

(vi) 6x + 3y = 6xy
2x + 4y = 5xy

(vii) 10/x+y + 2/x-y = 4
15/x+y – 5/x-y = -2

(viii) 1/3x+y + 1/3x-y = 3/4
1/2(3x-y) – 1/2(3x-y) = -1/8
 

Answer:

(i) … (1)

… (2)

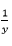Let =p and =q

then the equations becomes.

Using cross-multiplication method,we obtain,

⇒p = 2 andq = 3

(ii) 

Let =p and =q

Putting this in (1) and (2), we get

2p + 3q = 2 … (i)

4p − 9q = −1 … (ii)

Multiplying (i) by 3, we get

6p + 9q =6 … (iii)

Adding equation (ii) and (iii),we obtain

10p =5

p = 

Putting value of p in (i), we get

Hence,x = 4 and y = 9.

(iii) + 3y = 14

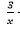− 4y = 23 and Let =p

Putting value of p in equation, we get

4p + 3y = 14 … (i)

3p − 4y = 23 … (ii)

By cross-multiplication,we get

Also, 

(iv)

putting= p and=q,we get,

=5p+q =2 … (i)
=6p-3q =1 … (ii)

Now, multiplying equation (i) by 3,we get

15p +3q = 6 … (iii)

Adding equation (ii) and (iii)

21 p = 7

p =

putting value of p in equation (iii),we get,

= -3q = -1

q =

we know that,
p =
= 3 = x – 1
= x = 4

q =

=y – 2 = 3
y = 5

Hence,x=4 and y =5

(v) 7x − 2y = 5xy … (1)

8x + 7y = 15xy … (2)

Dividing both the equations by xy, we get

… (i)

… (ii)

putting =p and =q

we get,

7q − 2p = 5 … (iii)

8q + 7p = 15 … (iv)

multiplying equation (iii) by 7 and equation (iv) by 2,we get,

49q – 14p =5 … (v)

16q + 14p = 30 … (vi)

After adding equation (v) and (vi),we get,
65q = 65
=q = 1

putting value of q in equation (iv), we get,

8 + 7p = 15
= 7p = 15 -8 = 7
= p =1

Now,
p = 

q = 

Hence,x = 1 and y = 1

(vi) 6x + 3y − 6xy = 0 … (1)

2x + 4y − 5xy = 0 … (2)

Dividing both the equations by xy, we get

Let =p and =q

Putting these in (3) and (4), we get

6q + 3p – 6 = 0 … (5)

2q + 4p – 5 = 0 … (6)

From (5),

3p = 6 − 6q

⇒p = 2 − 2q

Putting this in (6), we get

2q + 4 (2 − 2q) – 5 = 0

⇒ 2q + 8 − 8q – 5 = 0

⇒ −6q = −3⇒q = ½

Putting value of q in (p = 2 – 2q), we get

p = 2 – 2 (½) = 2 – 1 = 1

Putting values of p and q in (=p and =q), we getx = 1 andy = 2

(vii) … (1)

…(2)

Let

Putting this in (1) and (2), we get

10p + 2q = 4 … (3)

15p − 5q = −2 … (4)

From equation (3),

2q = 4 − 10p

⇒q = 2 − 5p … (5)

Putting this in (4), we get

15p – 5 (2 − 5p) = −2

⇒ 15p – 10 + 25p = −2

⇒ 40p = 8⇒p = 

Putting value of p in (5), we get

q = 2 – 5 () = 2 – 1 = 1

Putting values of p and q in (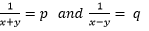), we get

⇒x +y = 5 … (6) andx –y = 1 … (7)

Adding (6) and (7), we get

2x = 6 ⇒x = 3

Puttingx = 3 in (7), we get

3 –y = 1

⇒y = 3 – 1 = 2

Therefore,x = 3 andy = 2

(viii)… (1)

… (2)

Let

Putting this in (1) and (2), we get

p +q = 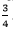and 

⇒ 4p + 4q = 3 … (3) and 4p − 4q = −1 … (4)

Adding (3) and (4), we get

8p = 2 ⇒p = ¼

Putting value of p in (3), we get

4 (¼) + 4q = 3

⇒ 1 + 4q = 3

⇒ 4q = 3 – 1 = 2

⇒q = ½

Putting value of p and q,we get,

⇒ 3x +y = 4 … (5) and 3x –y = 2 … (6)

Adding (5) and (6), we get

6x = 6 ⇒x = 1

Puttingx = 1 in (5) , we get

3 (1) +y = 4

⇒y = 4 – 3 = 1

Therefore,x = 1 andy = 1

2. Formulate the following problems as a part of equations, and hence find their solutions.

(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.

(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days.Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.

(iii) Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.

Answer:

(i) Let speed of rowing in still water =x km/h

Let speed of current =y km/h

So, speed of rowing downstream = (x +y) km/h

And, speed of rowing upstream = (x −y) km/h

According to given conditions,

2(x+y) = 20 and 2(x-y) = 4

⇒ 2x + 2y = 20 and 2x − 2y = 4

⇒x +y = 10 … (1) andx –y = 2 … (2)

Adding (1) and (2), we get

2x = 12⇒x = 6

Puttingx = 6 in (1), we get

6 +y = 10

⇒y = 10 – 6 = 4

Therefore, speed of rowing in still water = 6 km/h

Speed of current = 4 km/h

(ii) Let time taken by 1 woman alone to finish the work =x days

Let time taken by 1 man alone to finish the work =y days

Therefore,work done by a woman in 1 day =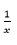

work done by a man in 1 day =

According to the question,

putting = p and  = q, in these equations
we obtain,

2p + 5q =
8p + 20q = 1

3p + 6q = 
= 9p + 18q = 1

By cross-multiplication,we obtain

x = 18, y = 36
Hence, number of days taken by a woman = 18 Number of days taken by a man = 36

(iii) Let speed of train =x km/h and let speed of bus =y km/h

According to given conditions,

putting in these equations,we obtain

Putting this in the above equations, we get

60p + 240q = 4 … (3)

And 100p + 200q = 

600p + 1200q = 25 … (4)

Multiplying (3) by 10, we get

600p +2400q = 40 … (5)

substracting equation (4) from (5),we obtain
1200q =15
q =… (6)

Substituting in equation(3),we obtain
60p + 3 = 4
60p = 1

u = 60km/h and v = 80km/h
Hence,speed of train = 60 km/h
speed of bus = 80km/h

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2