Solve the followings Questions.

1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following.

(i) p(x) = x³ – 3x² + 5x – 3 , g(x) = x² – 2

(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² – x + 1

(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 -x²

Answer:

(i)p(x) = x³ – 3x² + 5x – 3 , g(x) = x² – 2

Therefore, quotient = x – 3 and Remainder = 7x – 9

(ii)

Therefore, quotient = x² + x – 3 and Remainder = 8

(iii)

Therefore, quotient = -x² – 2 and, Remainder = −5x + 10

2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.

(i) t² – 3, 2t⁴ + 3t² – 9t -12

(ii) x² + 3x +1, 3x⁴ + 5x³ – 7x² + 2x + 2

(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x +1

Answer:

(i) t² – 3, 2t⁴ + 3t² – 9t -12

Remainder = 0

Hence first polynomial is a factor of second polynomial.

(ii) x² + 3x +1, 3x⁴ + 5x³ – 7x² + 2x + 2

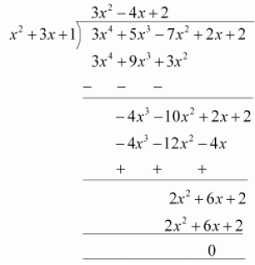
Remainder = 0

Hence first polynomial is a factor of second polynomial.

(iii)

Remainder ≠0

Hence first polynomial is not factor of second polynomial.

3. Obtain all other zeroes of ( 3×4 + 6×3 – 2×2 – 10x – 5 ) , if two of its zeroes are √5/3 and -√5/3.

Answer:

Two zeroes of ( 3x⁴ + 6x³ – 2x² – 10x – 5 ) are √5/3 and -√5/3 which means thatis a factor of ( 3x⁴ + 6x³ – 2x² – 10x – 5 ).

Therefore, we divide the given polynomial by x² – 5/3.

we factorize x² + 2x + 1 = (x + 1)²

Therefore, its zero is given by x + 1 = 0

⇒ x = – 1

As it has the term (x + 1)²,therefore, there will be 2 zeros at x = – 1.

Hence,the zeroes of the given polynomial √5/3 and -√5/3  are −1 and −1.

4. On dividing ( x³ – 3x² + x + 2 ) by a polynomial g(x), the quotient and remainder were (x-2) and (-2x+4) respectively. Find g(x).

Answer:

Let p(x) = x³ – 3x² + x + 2, q(x) = (x – 2) and r(x) = (–2x+4)

According to Polynomial Division Algorithm, we have

p(x) = g(x).q(x) + r(x)

⇒ x³ – 3x² + x + 2 =g(x).(x−2)−2x+4

⇒x³ – 3x² + x + 2 + 2x −4 =g(x).(x−2)

⇒x³ – 3x² + 3x + 2=g(x).(x−2)

So, Dividing x³ – 3x² + 3x + 2 by (x−2), we get

(x² – x + 1)

Therefore, we haveg(x) = (x² – x + 1)

5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and

(i) deg p(x) = deg q(x)

(ii) deg q(x) = deg r(x)

(iii) deg r(x) = 0

Answer:

Here let us represent, p(x) =dividend=the number to be divided

g(x)=Divisor=the number by which dividend is divided

q(x)=quotient

And r(x)=remainder

Now we have to give examples of polynomials such that the division algorithm

Dividend=Divisor × Quotient +Remainder

Is satisfies and the given conditions are also satisfied

(i)Let us assume the division of 2x + 4 by 2,

Then p(x) = 2x + 4

g(x) = 2

q(x) = x + 2

and r(x) = 0

On using the division algorithm

Dividend=Divisor × Quotient +Remainder

 p(x)=g(x) × q(x) +r(x)

On putting the given values we get,

=> 2x + 4 = 2 x (x +2) + 0

On solving we get,

=> 2x + 4 = 2x + 4

Hence the division algorithm is satisfied.

And here the degree of p(x) =1 = degree of q(x)

Hence (i) condition is also satisfied.

(ii) Let us assume the division of x³ + x byx²

Then here,p(x) = x³+ x

g(x) = x²

q(x) = x

r(x) = x

It is clear that the degree of q(x) = 1 and

degree of r(x) = 1

on using the devision algorithm

=> Dividend=Divisor × Quotient +Remainder

=> p(x)=g(x) × q(x) +r(x)

On putting the given values we get,

=> x³ + x = (x² * x) + x

on solving we get,

x³ + x = x ³ + x

Hence the division algorithm is satisfied.

and here the degree of r(x) = 1 = degree of q(x)

Hence (ii) condition is also satisfied.

(iii)Let us assume the division of x² + 1 byx

Then here,p(x) = x² + 1

g(x) = x

r(x) = 1

It is clear that the degree of r(x) = 0 and

on using the devision algorithm

=> Dividend=Divisor × Quotient +Remainder

=> p(x)=g(x) × q(x) +r(x)

On putting the given values we get,

=> x² + 1 = (x * x)+ 1

x² + 1 = x² + 1

Hence,the division algorithm is satisfied.

And here the degree of r(x) = 0

Hence (iii) condition is also satisfied.

 Here you can also assume any other polynomial for division but it is necessary that the chosen dividend and divisor be such that the conditions of the questions are satisfied.

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2