Solve the followings Questions.

In Q 1 to 3, choose the correct option and give justification.

1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is:

(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm

Answer:

(A) 

Let O be the centre of the circle.

Given that,

OQ = 25cm and PQ = 24 cm

As the radius is perpendicular to the tangent at the point of contact,

Therefore, OP ⊥ PQ

Applying Pythagoras theorem in ΔOPQ, we obtain

In right triangle OPQ,

[By Pythagoras theorem]

OP = 7 cm

Therefore, the radius of the circle is 7 cm.

Hence, alternative 7 cm is correct.

2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°

Answer:

(B) It is given that TP and TQ are tangents.

Therefore, radius drawn to these tangents will be perpendicular to the tangents.

Thus, OP ⊥ TP and OQ ⊥ TQ

∠OPT = 90º

∠OQT = 90º

In quadrilateral POQT,

Sum of all interior angles = 360°

∠OPT + ∠POQ +∠OQT + ∠PTQ = 360°

⇒ 90°+ 110º + 90° +∠PTQ = 360°

⇒ ∠PTQ = 70°

Hence, alternative 70° is correct.

3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠ POA is equal to
(A) 50°  
(B) 60°
(C) 70°
(D) 80°

Answer:

(A)It is given that PA and PB are tangents.

Therefore, the radius drawn to these tangents will be perpendicular to the tangents.

Thus, OA ⊥ PA and OB ⊥ PB

∠OBP = 90º

∠OAP = 90º

In AOBP,

Sum of all interior angles = 360°

∠OAP + ∠APB +∠PBO + ∠BOA = 360°

90° + 80° +90º +∠BOA = 360°

∠BOA = 100°

In ΔOPB and ΔOPA,

AP = BP (Tangents from a point)

OA = OB (Radii of the circle)

OP = OP (Common side)

Therefore, ΔOPB ≅ ΔOPA (SSS congruence criterion)

A ↔ B, P ↔ P, O ↔ O

And thus, ∠POB = ∠POA

Hence, alternative 50° is correct.

4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Answer:

Given: CD and EF are the tangents at the end points A and B of the diameter AB of a circle with centre O.

To prove: CD || EF.

Proof: CD is the tangent to the circle at the point A.

∴ ∠BAD = 90°

EF is the tangent to the circle at the point B.

∴ ∠ABE = 90°

Thus, ∠BAD = ∠ABE (each equal to 90°).

But these are alternate interior angles.

∴ CD || EF

5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Answer:

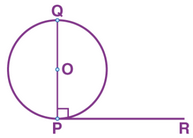
Let, O is the centre of the given circle.

A tangent PR has been drawn touching the circle at point P.

Draw QP ⊥ RP at point P, such that point Q lies on the circle.

∠OPR = 90° (radius ⊥ tangent)

Also, ∠QPR = 90° (Given)

∴ ∠OPR = ∠QPR

Now, the above case is possible only when centre O lies on the line QP.

Hence, perpendicular at the point of contact to the tangent to a circle passes through the centre of the circle.

6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Answer:

Since, the tangent at any point of a circle is perpendicular to radius through the point of contact.

Therefore, ∠OPQ = 90°

It is given that OQ = 5 cm

and    PQ = 4 cm

In right ΔOPQ, we have

OQ ² =OP ² +PQ ²
[Using Pythagoras Theorem]
OP ² = (5) ² – (4) ²

^{= 25 – 16 =9}

^{⇒ OP = 3 cm}

^{Hence, the radius of the circle is 3 cm.}

7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Answer:

Given Two circles have the same center O and AB is a chord of the larger circle touching the smaller circle at C; also. OA = 5 cm and OC = 3 cm

In Δ OAC,

⇒ AC = 4cm

∴ AB = 2AC (Since perpendicular drawn from the center of the circle bisects the chord)

∴ AB = 2 × 4 =  8cm

The length of the chord of the larger circle is 8 cm.

8. A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that:

AB + CD = AD + BC

Answer:

We know that the tangents from an external point to a circle are equal.

AP = AS ……….(i)

BP = BQ ……….(ii)

CR = CQ ……….(iii)

DR = DS……….(iv)

On adding eq. (i), (ii), (iii) and (iv), we get

(AP + BP) + (CR + DR)

= (AS + BQ) + (CQ + DS)

->AB + CD = (AS + DS) + (BQ + CQ)

so,AB + CD = AD + BC

9. In figure, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°.

Answer:

Given: In figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another

tangent AB with point of contact C intersecting XY at A and X’Y’ at B.

Let us join point O to C.

In ΔOPA and ΔOCA,

OP = OC (Radii of the same circle)

AP = AC (Tangents from point A)

AO = AO (Common side)

ΔOPA ≅ ΔOCA (SSS congruence criterion)

Therefore, P ↔ C, A ↔ A, O ↔ O

∠POA = ∠COA …(i)

Similarly, ΔOQB ≅ ΔOCB

∠QOB = ∠COB …(ii)

Since POQ is a diameter of the circle, it is a straight line.

Therefore, ∠POA + ∠COA + ∠COB + ∠QOB = 180º

From equations (i) and  (ii),it can be observed that

2∠COA + 2 ∠COB = 180º

∠COA + ∠COB = 90º

∠AOB = 90°

10. Prove that the angel between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.

Answer:

 Let us Consider a circle with centre O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment, joining point of contacts A and B together such that it subtends ∠AOB at center O of the circle.

It can be observed that

OA ⊥ PA

∴ ∠OAP = 90°

Similarly, OB ⊥ PB

∴ ∠OBP = 90°

In quadrilateral OAPB,

Sum of all interior angles = 360º

∠OAP +∠APB +∠PBO +∠BOA = 360º

⇒ 90º + ∠APB + 90º + ∠BOA = 360º

⇒ ∠APB + ∠BOA = 180º

∴ The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.

11. Prove that the parallelogram circumscribing a circle is a rhombus.

Answer:

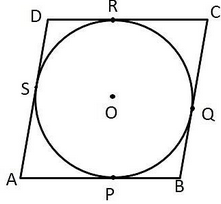
Given: ABCD is a parallelogram circumscribing a circle.

To Prove: ABCD is a rhombus.

Proof: Since, the tangents from an external point to a circle are equal.

We know that the tangents drawn to a circle from an exterior point are equal in length.

∴ AP = AS, BP = BQ, CR = CQ and DR = DS.

AP + BP + CR + DR = AS + BQ + CQ + DS

(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)

 ∴ AB + CD = AD + BC or 2AB = 2BC            (since AB = DC and AD = BC)

∴ AB = BC = DC = AD.

Therefore, ABCD is a rhombus.

Hence, proved.

12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.

Answer:

In ΔABC,

Length of two tangents drawn from the same point to the circle are equal,

∴ CF = CD = 6cm

∴ BE = BD = 8cm

∴ AE = AF =x

We observed that,

13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Answer:

Let ABCD be a quadrilateral circumscribing a circle with O such that it touches the circle at point P, Q, R, S. Join the vertices of the quadrilateral ABCD to the center of the circle.
In ΔOAP and ΔOAS,
AP = AS (Tangents from the same point)
OP = OS (Radii of the circle)
OA = OA (Common side)
ΔOAP ≅ ΔOAS (SSS congruence condition)
∴ ∠POA = ∠AOS
⇒∠1 = ∠8
Similarly we get,
∠2 = ∠3
∠4 = ∠5
∠6 = ∠7
Adding all these angles,
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 +∠8 = 360º
⇒ (∠1 + ∠8) + (∠2 + ∠3) + (∠4 + ∠5) + (∠6 + ∠7) = 360º
⇒ 2 ∠1 + 2 ∠2 + 2 ∠5 + 2 ∠6 = 360º
⇒ 2(∠1 + ∠2) + 2(∠5 + ∠6) = 360º
⇒ (∠1 + ∠2) + (∠5 + ∠6) = 180º
⇒ ∠AOB + ∠COD = 180º
Similarly, we can prove that ∠ BOC + ∠ DOA = 180º
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2