Solve the followings Questions.

1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating decimal expansion.

(i) 

(ii) 

(iii) 

(iv) 

(v) 

(vi) 

(vii) 

(viii) 

(ix) 

(x) 

Answer:

(i) 

q = 3125 = 5 x 5 x 5 x 5 x 5 = 5⁵

Here, denominator is of the form , where m = 5 and n = 0.

It means rational number   has a terminating decimal expansion.

(ii) 

q = 8 = 2 x 2 x 2 = 2³

Here, denominator is of the form , where m = 0 and n = 3.

It means rational number has a terminating decimal expansion.

(iii) 

q =  

Here, denominator is not of the, where m and n are non-negative integers.

It means rational number has a non-terminating repeating decimal expansion.

(iv) 

q = 1600 = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 5 =2⁶ x 5 x 5

Here, denominator is of the form , where m = 1 and n = 6.

It means rational number has a terminating decimal expansion.

(v) 

q = 343 = 7 x 7 x 7

Here, denominator is not of the form , where m and n are non-negative integers.

It means rational number has non-terminating repeating decimal expansion.

(vi) 

q = 2 x 2 x 2 x 5 x 5

Here, denominator is of the form , where m = 2 and n = 3 are non-negative integers.

It means rational number   has terminating decimal expansion.

(vii) 

q = 2 x 2 x 5 x 5 x 5 x 5 x 5 x 5 x 5 x 7 x 7 x 7 x 7 x 7

Here, denominator is not of the form , where m and n are non-negative integers.

It means rational number has non-terminating repeating decimal expansion.

(viii) 

Here, denominator is of the form , where m = 1 and n = 0.

It means rational number has terminating decimal expansion.

(ix) 

q = 10 = 2 x 5

Here, denominator is of the form , where m = 1 and n = 1.

It means rational number has terminating decimal expansion.

(x) 

q = 30 = 2 x 3 x 5

Here, denominator is not of the form , where m and n are non-negative integers.

It means rational number has non-terminating repeating decimal expansion.

2. Write down the decimal expansions of those rational numbers in Question 1 which have terminating decimal expansions.

Answer:

(iv)

                                                                                            x

                                                                                    —————–

3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If, they are rational, and of the form , what can you say about the prime factors of q?

(i) 43.123456789

(ii) 0.120112001200 0120000…

(iii) 

Answer:

(i) 43.123456789

It is rational because decimal expansion is terminating. Therefore, it can be expressed in 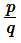form where factors of q are of the form where n and m are non-negative integers

(ii) 0.120112001200 0120000…

It is irrational because decimal expansion is neither terminating nor non-terminating repeating.

(iii) 

It is rational because decimal expansion is non-terminating repeating. Therefore, it can be expressed in 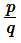form where factors of q are not of the form where n and m are non-negative integers.

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2