Solve the followings Questions.

Unless stated otherwise, use π =22/7

1. Find the area of the shaded region in figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.

Answer:

PQ = 24 cm and PR = 7 cm


∠P = 90° (Angle in the semi-circle)


∴ QR is hypotenuse of the circle = Diameter of the circle.


By Pythagoras theorem,


QR² = PR² + PQ²


⇒ QR² = 7² + 24²

⇒ QR² = 49 +576

⇒ QR² = 625

⇒ QR = 25cm


∴ Radius of the circle = 25/2cm


Area of the semicircle = (πR²)/2 


= (22/7 × 25/2 × 25/2)/2) cm²

= 13750/56 cm² = 245.54 cm²


Area of the ΔPQR = 1/2 × PR × PQ


= 1/2 × 7 × 24 cm²

= 84 cm²


Area of the shaded region


= Area of the semicircle – Area of the ΔPQR


= 245.54 cm² − 84 cm² = 161.54cm²
 

2. Find the area of the shaded region in figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.

Answer:

Given that,
Radius of the small circle, OB = 7 cm
Radius of second circle, OA = 14 cm
and ∠AOC = 40°

We know that, the area of a sector that subtends an angle θ at the centre of the circle is θ/360° × πr²
where, θ is in degrees.

∴ Area of minor sector OBD = 40/360 × 22/7 × 7 × 7     [∵ π = 22/7]

= 1/9 × 22 × 7

= 17.11 cm²

Also, area of minor sector OAC = 40/360 × 22/7 × 14 × 14

= 1/9 × 22 × 2 × 14

= 68.4 cm²

Now, area of the shaded region = Area of sector OAC − Area of sector OBD

= 68.4 − 17.1

= 51.3 cm²

Hence, the area of the shaded region is 51.3 cm².
 

3. Find the area of the shaded region in figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.

Answer:

Area of the shaded region = Area of Square ABCD − (Area of semicircle APD + Area of semicircle BPC)

= (14)² − [1/2 π (14/2)² + 1/2 π (14/2)²]

= (14)² − 22/7 (7)²

= 196 − 154

= 42 cm²

Hence, the area of the shaded region is 42 cm².

4. Find the area of the shaded region in figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.

Answer:

Area of Shaded region = Area of equilateral triangle ABO + Area of Major sector


Area of Equilateral Triangle ABO = √3/4 × a² = √3/4 × 12 × 12 cm²



= 62.352 cm²


Area of major sector = θ/360 × π × r²

= 300/360 × π × 6 × 6 cm²
= 94.2 cm²

Area of Shaded region = 62.352 + 94.2 = 156.55 cm²
 

5. From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in figure. Find the area of the remaining portion of the figure.

Answer:

Side of the square = 4 cm
Radius of the circle = 1 cm
Four quadrant of a circle are cut from corner and one circle of radius are cut from middle.
Area of square = (side)² = 4² = 16 cm²
Area of the quadrant = (π R²)/4 cm² = (22/7 × 12)/4 = 11/14 cm²
∴ Total area of the 4 quadrants = 4 × (11/14) cm² = 22/7 cm²
Area of the circle = π R² cm² = (22/7 × 12) = 22/7 cm²
Area of the shaded region = Area of square – (Area of the 4 quadrants + Area of the circle)
= 16 cm² – (22/7 + 22/7) cm²
= 68/7 cm²

6. In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in figure. Find the area of the design (shaded region).

Answer:

cos θ = AD/OA

cos 30° = √3/2

AD = √3/2 × 32

AD = 16√3cm

AB = 32√3cm

shaded region = Area of circle – Area of triangle

= π(32)² − 3 × 1/2 × 32√3 × 16

= ((22578/7) − 768√3)cm²
 

7. In figure ABCD is a square of side 14 cm. With centers A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region.

Answer:

Side of square = 14 cm
Four quadrants are included in the four sides of the square.
∴ Radius of the circles = 14/2 cm = 7 cm
Area of the square ABCD = 14² = 196 cm²
Area of the quadrant = (π R2)/4 cm² = (22/7 × 72)/4 cm²
= 77/2 cm²
Total area of the quadrant = 4 × 77/2 cm² = 154 cm²

Area of the shaded region = Area of the square ABCD – Area of the quadrant
= 196 cm² – 154 cm²
= 42 cm²

8. Figure depicts a racing track whose left and right ends are semicircular.

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:

(i) the distance around the track along its inner edge.

(ii) the area of the track.

Answer:

(i) 
The distance around the track along its inner edge


= EG + FH + 2 × (circumference of the semicircle of radius OE = 30 cm)


= 106 + 106 + 2(1/2 × 2π × 30) = 212 + 60π


= 212 + 60 x 22/7 = (212+1320/7)m = (1484 + 1320)/7m = 2804/7m = (400)4/7m


(ii) 
Area of the track = Area of the shaded region


= Area of the rectangle AEGC + Area of the rectangle BFHD + 2 + (Area of the semicircle of radius 40 m − Area of the semicircle with radius 30 m−)


= [(10 × 106) + (10 × 106)] + 2{1/2 × 22/7 × (40)² − 1/2 × 22/7 × (30)²}


= 1060 + 1060 + 22/7 [(40)² − (30)²]


= 2120 + 22/7 × 700 = 2120 + 2200 = 4320 m²
 

9. In figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

Answer:

OD is diameter of smaller circle.



Area of the smaller circle


= π × 3.5² = 38.49 cm²



Area of ΔABC = 0.5 × (14)(7) = 49 cm²



Area of semi-circle = 0.5π(7)(7) = 76.97 cm²



Area of shaded portion in semi-circle = 76.97 − 49 = 27.97 cm²



Total required area = 38.49 + 27.97 = 66.46 cm²
 

10. The area of an equilateral triangle ABC is 17320.5 cm². With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Figure ). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)

Answer:

Let the side of the equilateral triangle be a.
Area of equilateral triangle = 17320.5 cm²
√3/4 (a)² = 17320.5

1.73205/4 a² = 17320.5

a² = 4 x 10000

a = 200 cm

Each sector is of measure 60°.
Area of sector ADEF = 60°/360° x π x r²

= 1/6 x π x (100)²

= (3.14 x 10000)/6

= 15700/3 cm²

Area of shaded region = Area of equilateral triangle − 3 × Area of each sector

= 17320.5 – 3 x 15700/3
= 17320.5 – 15700 = 1620.5 cm²
 

11. On a square handkerchief, nine circular designs each of radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.

Answer:

Side of square = 3 × diameter of 1 circle
= 3 × 14 = 42cm

Area of remaining portion = Area of square – 9 × area of 1 circle

= (42 × 42) – 9 × 22/7 × 7 × 7

= 1764 − 1386

= 378 cm²

 

12. In figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the:

(i) quadrant OACB

(ii) shaded region

Answer:

(i) Area of quadrant OACB = Area of Circle/4 = (π × r²)/4 = 1/4 × 22/7 × 3.5 × 3.5

= 9.625cm²

(ii) Area of the shaded region = Area of Quadrant − Area of △BDO

= 9.625 − (1/2 × 3.5 × 2)

= 6.125 cm²

 

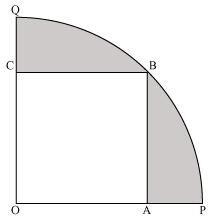
13. In figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)

Answer:

Side of square = OA = AB = 20 cm
Radius of the quadrant = OB
OAB is right angled triangle
By Pythagoras theorem in ΔOAB ,
OB² = AB²  + OA²
⇒ OB² = 20²  + 20²
⇒ OB² = 400  + 400
⇒ OB² = 800
⇒ OB = 20√2 cm
Area of the quadrant = (πR2)/4 cm² = 3.14/4 × (20√2)² cm² = 628 cm²
Area of the square = 20 × 20 = 400  cm²

Area of the shaded region = Area of the quadrant – Area of the square
= 628 – 400 cm² = 228 cm²

14. AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig. ). If ∠AOB = 30°, find the area of the shaded region.

Answer:

Radius of the larger sector, R=21 cm


Radius of the smaller sector, r=7 cm


Angle subtended by sectors of both concentric circles = 30°



Area of the sector making angle θ


= (θ/360°) × πr²



Area of the larger sector

= (30°/360°) × πR²cm²
= 1/12 × 22/7 × 21² cm²
= 1/12 × 22/7 × 21 × 21 cm²
= 231/2 cm²



Area of the smaller circle

= (30°/360°) × πr² cm²
= 1/12 × 22/7 × 7² cm²
= 1/12 × 22/7 × 7 × 7 cm²
= 77/6 cm²



Area of the shaded region = Area of the larger sector − Area of the smaller sector


= (231/2 − 77/6) cm²
= 616/6 cm²
= 308/3 cm²
= (102) 2/3 cm²
 

15. In figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

Answer:

Radius of the the quadrant ABC of circle = 14 cm
AB = AC = 14 cm
BC is diameter of semicircle.
ABC is right angled triangle.
By Pythagoras theorem in ΔABC,
BC² = AB²  + AC²
⇒ BC² = 14²  + 14²
⇒ BC = 14√2 cm
Radius of semicircle = 14√2/2 cm = 7√2 cm

Area of ΔABC = 1/2 × 14 × 14 = 98 cm²
Area of quadrant = 1/4 × 22/7 × 14 × 14 = 154 cm²
Area of the semicircle = 1/2 × 22/7 × 7√2 × 7√2 = 154 cm²

Area of the shaded region = Area of the semicircle + Area of ΔABC – Area of quadrant
= 154 + 98 – 154 cm² = 98 cm²

16. Calculate the area of the designed region in figure common between the two quadrants of circles of radius 8 cm each.

Answer:

AB = BC = CD = AD = 8 cm

Area of ΔABC = Area of ΔADC = 1/2 × 8 × 8 = 32 cm²
Area of quadrant AECB = Area of quadrant AFCD = 1/4 × 22/7 × 8²
= 352/7 cm²

Area of shaded region = (Area of quadrant AECB – Area of ΔABC) +(Area of quadrant AFCD – Area of ΔADC)
= (352/7 – 32) + (352/7 -32) cm²
= 2 × (352/7 -32) cm²
=  256/7 cm²

CHAPTER NAME	OLD NCERT	NEW NCERT
Real Numbers	EXERCISE 1.1
	EXERCISE 1.2	1.1	CLICK HERE
	EXERCISE 1.3	1.2	CLICK HERE
	EXERCISE 1.4
Polynomials	EXERCISE 2.1	2.1	CLICK HERE
	EXERCISE 2.2	2.2	CLICK HERE
	EXERCISE 2.3
	EXERCISE 2.4
Pair of Linear Equations in Two Variables	EXERCISE 3.1
	EXERCISE 3.2	3.1	CLICK HERE
	EXERCISE 3.3	3.2	CLICK HERE
	EXERCISE 3.4	3.3	CLICK HERE
	EXERCISE 3.5
	EXERCISE 3.6
	EXERCISE 3.7
Quadratic Equations	EXERCISE 4.1	4.1	CLICK HERE
	EXERCISE 4.2	4.2	CLICK HERE
	EXERCISE 4.3
	EXERCISE 4.4	4.3	CLICK HERE
Arithmetic Progressions	EXERCISE 5.1	5.1	CLICK HERE
	EXERCISE 5.2	5.2	CLICK HERE
	EXERCISE 5.3	5.3	CLICK HERE
	EXERCISE 5.4	5.4 (Optional)	CLICK HERE
Triangles	EXERCISE 6.1	6.1	CLICK HERE
	EXERCISE 6.2	6.2	CLICK HERE
	EXERCISE 6.3	6.3	CLICK HERE
	EXERCISE 6.4
	EXERCISE 6.5
	EXERCISE 6.6
Coordinate Geometry	EXERCISE 7.1	7.1	CLICK HERE
	EXERCISE 7.2	7.2	CLICK HERE
	EXERCISE 7.3
	EXERCISE 7.4
Introduction to Trigonometry	EXERCISE 8.1	8.1	CLICK HERE
	EXERCISE 8.2	8.2	CLICK HERE
	EXERCISE 8.3
	EXERCISE 8.4	8.3	CLICK HERE
Some Applications of Trigonometry	EXERCISE 9.1	9.1	CLICK HERE
Circles	EXERCISE 10.1	10.1	CLICK HERE
	EXERCISE 10.2	10.2	CLICK HERE
Construction
Areas Related to Circles	EXERCISE 12.1
	EXERCISE 12.2	11.1	CLICK HERE
	EXERCISE 12.3
Surface Areas and Volumes	EXERCISE 13.1	12.1	CLICK HERE
	EXERCISE 13.2	12.2	CLICK HERE
	EXERCISE 13.3
	EXERCISE 13.4
	EXERCISE 13.5
Statistics	EXERCISE 14.1	13.1	CLICK HERE
	EXERCISE 14.2	13.2	CLICK HERE
	EXERCISE 14.3	13.3	CLICK HERE
	EXERCISE 14.4
Probability	EXERCISE 15.1	14.1	CLICK HERE
	EXERCISE 15.2